Solving My First CTF Challenges on Pwnable.kr

I recently started solving some Capture The Flag (CTF) challenges and decided to document them on my blog. These challenges are a great way to learn a lot about low-level programming, security, and reverse engineering.

Getting Started with Pwnable.kr

I came across pwnable.kr through the Low Level YouTube channel and decided to give it a try. Today, I attempted the first two challenges, and I must say—they were exciting and eye-opening.

Challenge 1: File Descriptor Trick

The first challenge was relatively easy. It revolves around understanding file descriptors in Linux. In Unix-like systems, standard input (stdin) has a file descriptor of 0. The program contains a calculation like:

entered_value - 0x1234 = fd

Since the file descriptor for stdin is 0, solving for entered_value gives:

entered_value = 0x1234 = 4660

So I simply entered 4660 as the input, and the challenge was solved. A great warm-up!

Challenge 2: Hash Collision

The second challenge requires us to create a hash collision using a very basic hashing algorithm. Here’s the C code provided:

unsigned long check_password(const char* p) {
    int* ip = (int*)p;
    int i;
    int res = 0;
    for(i = 0; i < 5; i++) {
        res += ip[i];
    }
    return res;
}

This code is particularly interesting because of the line int* ip = (int*)p;. Here, p is a char*, meaning it’s interpreted as an array of 1-byte characters. But when cast to an int*, it reads 4 bytes at a time, treating each group of 4 characters as a single integer.

To understand this behavior, I created a small C program and used the string "AAAA". Since the ASCII value of ‘A’ is 0x41, it printed 0x41414141 when I used printf("%x", p[0]). Then I tried "BAAA" and noticed that the result was 0x41414142, indicating a little-endian system where the least significant byte is stored first.

Understanding Endianness

To better understand the behavior of the hash function, it’s important to grasp the concept of endianness:

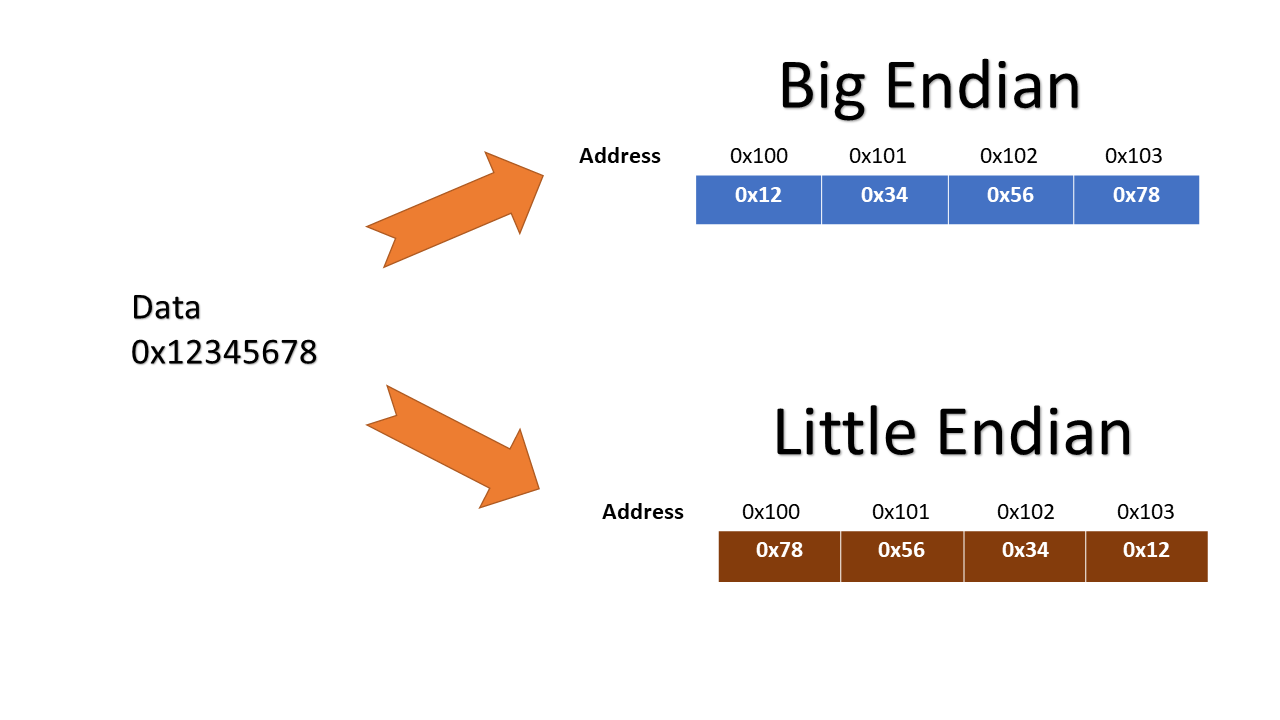
In my case, the system was using little-endian byte order, where the least significant byte is stored at the lowest memory address. This affected how the characters in my input string were interpreted when cast from char* to int*:

This endianness knowledge was crucial for crafting the right input string to produce the target hash value.

Objective

The goal of the challenge is to craft a string that, when passed into the hashing function above, results in the hash value 0x21DD09EC.

Approach

To solve it, I broke down the hash value into its hexadecimal components:

• EC
• 09
• DD
• 21

Then, I worked from the least significant byte to the most significant byte. While doing this, I had to consider how carry bits affect the higher-order values. For the most significant byte (21), I didn’t worry about the carry because it gets dropped due to integer overflow.

I also had to ensure that the characters I used were printable and valid ASCII characters. After several attempts and tweaking, I finally crafted this string:

B22322232223#2#3#A#U

This string produces the exact hash 0x21DD09EC.

Final Thoughts

I successfully completed both challenges! 🎉

The first one was a nice introduction, and the second one had much more to explore and learn from. There might be more elegant or efficient ways to solve these challenges, and I will update this article if I discover any. For now, I’m just thrilled to be diving into CTFs and learning so much from them.